Этот пост по сути является введением в такую востребованную дисциплину, как “квантовая механика для чайников” и это будет попыткой еще раз показать отличие квантовых вероятностей от классических. Надеюсь, что эта заметка сможет помочь какому нибудь третьекурснику разобраться в дираковских <бра| и |кет> обозначениях.

Итак, пусть имеется некая квантовая система (например, атомное ядро), которая может находиться в двух разных состояниях (|распалось>, |еще_не_распалось>). Основной постулат квантовой механики гласит о том, что если система может находиться в двух указанных выше состояниях, то она может находиться и в состоянии a|распалось> + b|еще_не_распалось>, где a и b – численные коэффициенты (возможно, комплексные). Если эта квантовая система посредством некоего устройства (ампулы с ядом) связана с котом так, что одно из состояний системы соответствует тому, что устройство не сработало и кот жив, а другое состояние системы отвечает тому, что кот мертв (ядро распалось и ампула разбилась), то и кот, таким образом, вместе запертой вместе с ним квантовой системой находится в двух состояниях одновременно. Состояние кота ![]() может быть:
может быть:
1) ![]() – кот живой
– кот живой
2) ![]() – кот мертвый
– кот мертвый
и, как было указано выше, кот может быть одновременно живым и мертвым:
(1) ![]()
Где, ![]() и
и ![]() – некие комплексные числа. При этом, при “открытии коробки” (измерении состояния кота) мы обнаружим его живым с вероятностью
– некие комплексные числа. При этом, при “открытии коробки” (измерении состояния кота) мы обнаружим его живым с вероятностью ![]() и мертвым с вероятностью
и мертвым с вероятностью ![]() Естественно, что
Естественно, что ![]() . Весь этот пост посвящен тому, чтобы объяснить разницу между утверждениями:
. Весь этот пост посвящен тому, чтобы объяснить разницу между утверждениями:
1) Измерение состояния кота даст результат
с вероятностью
и
с вероятностью
.
2) Кот в закрытой коробке находится в состоянии:с вероятностью
или
с вероятностью
.
Быстрый ответ для тех, кому лень продираться пусть и через простую, но математику.
В первом случае (“квантовая вероятность”) мы можем (хотя бы чисто теоретически) измерить состояние кота в другом базисе так, чтобы отвечать не на вопрос “состояние кота живой или мертвый?”, а отвечать на вопрос типа “состояние кота полуживой или полумертвый?”. И если мы правильно подберем вопрос (степень полуживости или полумертвости), то мы будем получать результат со 100% вероятностью – никакой случайности в результатах измерения не останется. Во втором же варианте никаким изменением постановки вопроса добиться исчезновения случайности невозможно – это суть классическое незнание и классические вероятности.
А теперь, информация для тех, кому не лень и для вышеупомянутых третьекурсников 🙂
1. Квантовый кот.

Каждому состоянию кота ![]() можно сопоставить, как бы это выразиться – “отражения” этих состояний:
можно сопоставить, как бы это выразиться – “отражения” этих состояний: ![]() . Как, скажем, каждому человеку можно сопоставить его отражение в зеркале и наоборот. Но в нашем случае, действуют следующие математические правила взаимодействия состояний и их “отражений” (или “отражений” других состояний). Если умножить отражение какого то состояния на другое состояние, то получится какое то число:
. Как, скажем, каждому человеку можно сопоставить его отражение в зеркале и наоборот. Но в нашем случае, действуют следующие математические правила взаимодействия состояний и их “отражений” (или “отражений” других состояний). Если умножить отражение какого то состояния на другое состояние, то получится какое то число:
![]()
Здесь число ![]() это результат умножения “отражения” состояния
это результат умножения “отражения” состояния ![]() на состояние
на состояние ![]() . Значок умножения
. Значок умножения ![]() принято не писать:
принято не писать:
![]()
“Состояние” и число – это объекты разной природы, но это не должно смущать, ведь из двух векторов точно также можно получить обыкновенное число путем скалярного умножения. Если мы поменяем местами “отражение” и состояние в приведенном выше примере, то число изменится на комплексно-сопряженное (звездочка):
![]()
А если мы перемножим состояние с собственным “отражением”, то получим не просто какое то число, а единицу:
(2) ![]()
А если перемножим состояние и отражение “ортогонального” состояния, то получим ноль:
(3) ![]()
В этом смысле “жизнь” и “смерть” ортогональны друг другу.
Минуточку, а как расписать подробнее вид “отражения” для состояния ![]() , зная как оно зависит от состояний
, зная как оно зависит от состояний ![]() и
и ![]() ? – очень просто:
? – очень просто:
Если
![]()
то
![]()
Перемножить состояние ![]() (1) с собственным “отражением” тоже легко:
(1) с собственным “отражением” тоже легко:
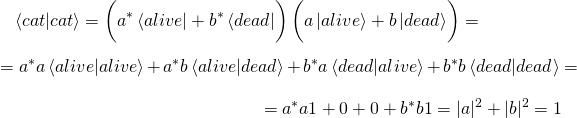
При этом были использованы соотношения (2), (3).
Итак, если состояние кота в закрытой коробке квантовое и равно ![]() , то вероятность
, то вероятность ![]() при открытии коробки обнаружить кота в состоянии “живой”
при открытии коробки обнаружить кота в состоянии “живой” ![]() равна:
равна:
(4) ![]()
При этом вероятность ![]() при открытии коробки обнаружить кота в его же текущем состоянии
при открытии коробки обнаружить кота в его же текущем состоянии ![]() равна:
равна:
![]()
Если в закрытой коробке лежит мертвый кот, т.е. ![]() , то согласно формуле (4), вероятность в этом случае обнаружить его живым при открытии коробки равна:
, то согласно формуле (4), вероятность в этом случае обнаружить его живым при открытии коробки равна:
![]()
А если состояние кота не ![]() , а
, а ![]() , то, как легко увидеть из формулы (4), вероятность обнаружить кота живым – по прежнему 100%. Общий минус перед состоянием ни на что не влияет.
, то, как легко увидеть из формулы (4), вероятность обнаружить кота живым – по прежнему 100%. Общий минус перед состоянием ни на что не влияет.
Представим себе, что из-за взаимодействия внутри коробки с квантовой системой состояние кота стало таким:
(5) ![]()
Легко проверить, что корни из двойки взялись не просто так, а для того, чтобы все было согласовано с данными выше определениями и постулатами. Действительно:
![]()
Вероятности обнаружить кота живым или мертвым равны 1/2. Используем указанное выше правило (4) и найдем вероятность обнаружить кота в состоянии (5) живым:
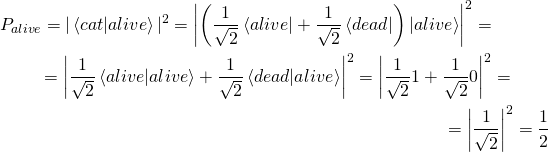
Введем следующие обозначения “полуживого” (![]() ) и “полумертвого” (
) и “полумертвого” (![]() ) кота:
) кота:
(6) ![]()
(7) ![]()
Легко убедиться, что состояния ![]() и
и ![]() ведут себя также как и
ведут себя также как и ![]() и
и ![]() (см. формулы (2), (3) ):
(см. формулы (2), (3) ):
(8) ![]()
(9) ![]()
То есть, состояниями “полуживой” и “полумертвый” точно так же можно описывать кота, как и состояниями “живой” и “мертвый”. Точно также, как в случае, когда состояние кота является “мертвый”, его невозможно обнаружить в состоянии “живой”, так и теперь, в случае, если состояние кота “полуживой”, то имеется нулевая вероятность обнаружить его в состоянии “полумертвый”. Однако, если состояние кота “мертвый”, то вероятность обнаружить его в состоянии “полуживой” (или “полумертвый”) равна 1/2. Если же кот находится в состоянии “полумертвый”, и мы не будем измерять “жив кот или мертв”, а будем измерять “полужив кот или полумертв”, то мы со 100% вероятностью получим ответ “полумертв”. В этом и заключается суть “квантовых” вероятностей: одно и то же состояние может давать либо разные результаты при измерениях с какими-то вероятностями, либо же один предсказуемый результат, если измерять специально подобранную величину.
Для лучшего понимания предлагаю посмотреть на картинку:
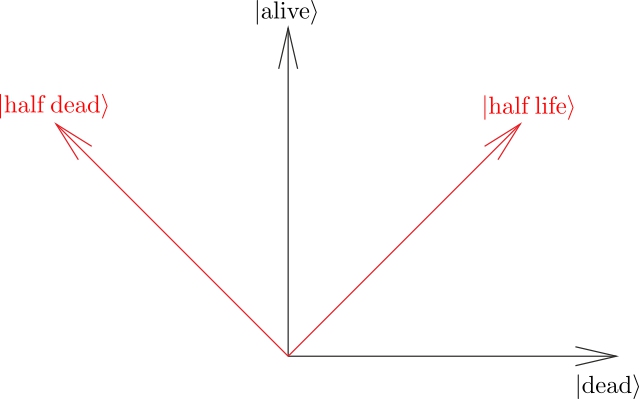
2. Обычный кот с налетом квантовости.

Въедливый читатель может задуматься, а почему это он “умножает” состояния и “отражения” так, что слева всегда идет “отражение”, а состояние справа? А если написать наоборот, то что будет? Напишем наоборот:
![]()
Вышеуказанный объект ![]() это не число, не состояние кота и не “отражение”, а оператор, который можно приписать рядом с состоянием или “отражением” так, чтобы изменить состояние или “отражение” на другие. Например, было состояние кота живой
это не число, не состояние кота и не “отражение”, а оператор, который можно приписать рядом с состоянием или “отражением” так, чтобы изменить состояние или “отражение” на другие. Например, было состояние кота живой ![]() и на него подействовали оператором
и на него подействовали оператором ![]() , так что получилось:
, так что получилось:
![]()
Вот так, оператор ![]() убил кота (подумайте, как записать оператор, который будет наоборот “оживлять” кота?). Можно задастся вопросом, а почему мы прилепили
убил кота (подумайте, как записать оператор, который будет наоборот “оживлять” кота?). Можно задастся вопросом, а почему мы прилепили ![]() слева от состояния
слева от состояния ![]() , а не справа? Не так:
, а не справа? Не так:
![]()
Дело в том, что если так написать, то мы получим два идущих подряд состояния: ![]() , а это в данной науке принимается как состояния двух разных котов. Когда мы описываем одного кота, то состояния, должны чередоваться с отражениями в произведениях. Легко понять, что оператор
, а это в данной науке принимается как состояния двух разных котов. Когда мы описываем одного кота, то состояния, должны чередоваться с отражениями в произведениях. Легко понять, что оператор ![]() может менять не только состояния, но и “отражения”. При этом оператор
может менять не только состояния, но и “отражения”. При этом оператор ![]() записывается справа от “отражения”, на которое он действует:
записывается справа от “отражения”, на которое он действует:
![]()
Заметьте, тот же самый оператор ![]() , который “убивал кота”, “оживляет” “отражение” мертвого кота, превращая его в отражение живого.
, который “убивал кота”, “оживляет” “отражение” мертвого кота, превращая его в отражение живого.
Важно: оказывается, состояния можно описывать не только вот такими векторами ![]() , но и операторами. Например, состоянию
, но и операторами. Например, состоянию ![]() (из формулы (1)) соответствует такой оператор:
(из формулы (1)) соответствует такой оператор:
![]()
Оператор ![]() называется “матрица плотности”. Ну да, скажете вы, что тут такого, приписали к состоянию его же “отражение” и получился оператор. И что дальше? А дальше можно заметить интересное свойство
называется “матрица плотности”. Ну да, скажете вы, что тут такого, приписали к состоянию его же “отражение” и получился оператор. И что дальше? А дальше можно заметить интересное свойство ![]() :
:
(10) 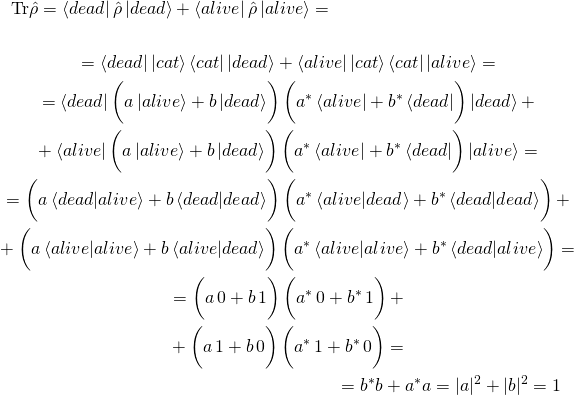
Точно так же, как и в случае формулы (4) высчитывать вероятности обнаружения кота живым в результате измерения его состояния. Итак, если мы знаем состояние кота, заданное матрицей плотности ![]() , то вероятность найти кота живым, в состоянии
, то вероятность найти кота живым, в состоянии ![]() равна:
равна:
(11) 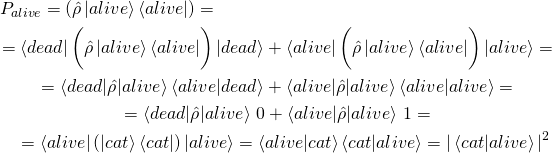
Результат получился в точности, как в формуле (4). Ну и зачем было все это нагромождать, если результат получается таким же? А затем, что с помощью матрицы плотности можно описывать не только квантовые состояния кота, но и классические. Например, мы хотим описать состояние кота, которому соответствует фраза:
Кот в закрытой коробке находится в состоянии:
с вероятностью
или
с вероятностью
Это состояние не квантовое, а классическое. Кот в коробке не жив и мертв одновременно, про что рассказывалось ранее, а вполне обыденно жив или мертв, только с какой то вероятностью. Вот какая матрица плотности соответствует этому состоянию:
![]()
Сравните это выражение с матрицей плотности для квантового кота ![]() (формула (1)):
(формула (1)):
(12) 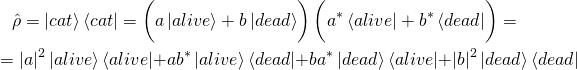
Видите, в квантовом случае матрица плотности содержит больше слагаемых, чем в классическом. Хотя, вероятность увидеть кота в состоянии ![]() одинакова и равна
одинакова и равна ![]() для двух, описанных выше примеров. Разница состоит в том, что если в случае квантового кота можно было (хотя бы умозрительно) проводить измерение не в базисе живой/мертвый, а в базисе полуживой/полумертвый, и таким образом можно было избавиться от случайности в результатах. А в в случае классического, не квантового кота, такой финт не пройдет – вероятности и случайности никуда не денутся.
для двух, описанных выше примеров. Разница состоит в том, что если в случае квантового кота можно было (хотя бы умозрительно) проводить измерение не в базисе живой/мертвый, а в базисе полуживой/полумертвый, и таким образом можно было избавиться от случайности в результатах. А в в случае классического, не квантового кота, такой финт не пройдет – вероятности и случайности никуда не денутся.