Не секрет, что в последнее время ведутся активные попытки построить квантовый компьютер. Вкратце, зачем это нужно. Доказано, что квантовый компьютер (когда будет построен) сможет за короткое время решать задачи, которые нынешние компьютеры (классические) могут решить лишь за тысячи лет непрерывной работы. Одной (и самой главной, из-за чего на исследования выделяются огромные деньги) из этих задач является нахождение простых множителей заданного числа (взлом шифрования с открытым ключом RSA). И, соответственно, создание новых, квантовых систем шифрования и защищенных линий связи. Возможен также и квантовый интернет, особенностью которого будут “запутанные” квантовые состояния, связывающие удаленные компьютеры между собой. А там, где новые компьютеры, там и новые игры.
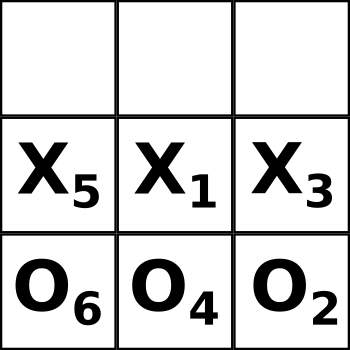
В этом посте я попытаюсь рассказать о двух “квантовых” вариантах простой игры в крестики-нолики. Играть в эти квантовые крестики нолики можно без всякого квантового компьютера. Квантовые крестики-нолики в данном случае важны как методическое указание, как простейший пример того, что такое квантовая суперпозиция и редукция волновой функции при измерении. Итак, для начала определимся с игровым полем – это обычные 3х3 девять клеток. Для дальнейшего удобства пронумеруем их вот так:

Первый вариант игры, который мы рассмотрим, был предложен в работе [Allan Goff, Am. J. Phys. 74, 962 (2006)]. Суть заключается в том, что каждый игрок может имеющийся у него крестик (или нолик) не просто поставить в свободную клетку, а распределить его в двух разных клетках. Рассмотрим пример игры. Пусть крестиками играет Боб, а ноликами играет Алиса. Боб ходит первым и ставит свой первый крестик в клетки 5 и 8:
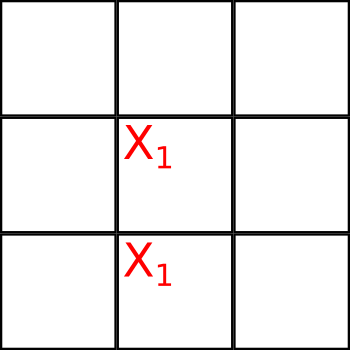
Здесь важно к крестикам/ноликам приписывать индексы – номера ходов.
Алиса делает следующий второй ход ноликом в клетки 5 и 9:
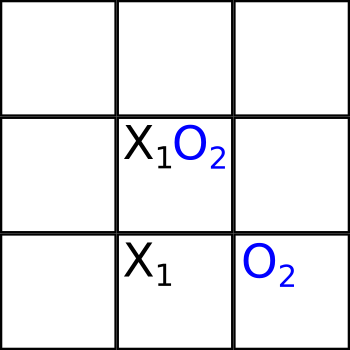
Заметьте, в клетке 5 уже стоял крестик, но так как это был не “полноценный” крестик, а только половинка (оригинальное название таких “недокрестиков/недоноликов” – spooky marks, т.е. призрачные ходы), то в эту же клетку можно ходить еще и еще другими половинками ноликов и крестиков. Теоретически, в клетке может быть 8 таких вот полу-ноликов и полу-крестиков (при этом другие половинки покрывают все остальные клетки).
Следующий третий ход Боба, он ставит крестик в клетки 5 и 6:
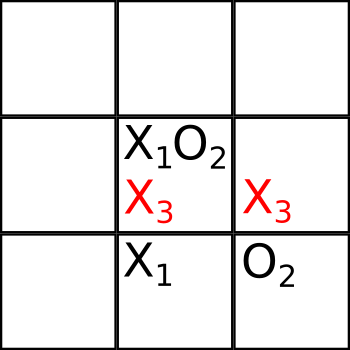
В клетке 5 уже скопилось три половинки (призрака)!
Но вот четвертый ход и ходит Алиса ноликом на клетки 6 и 8:
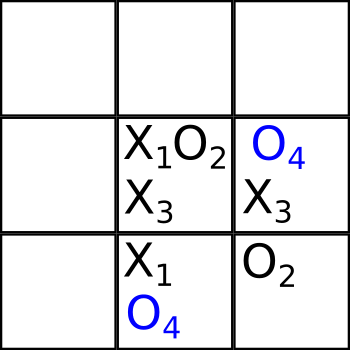
Это был не простой ход, Алиса замкнула “петлю связности” (cyclic entanglement) ходов {1,3,4}, вот она выделена желтым цветом и зелеными линиями:
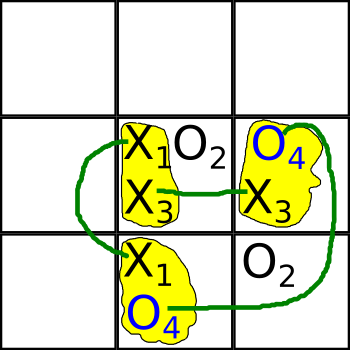
- Клетки 5 и 8 связаны посредством хода X1
- Клетки 8 и 6 связаны посредством хода O4
- Клетки 6 и 5 связаны посредством хода X3
То есть, у нас получился некий аналог “запутанного” состояния, который можно распутать с помощью “измерения”. Так как петлю закрыла Алиса, то выбирать способ (а он не один!) распутывания должен Боб. На этом этапе “распутывания” в клетках наконец то исчезают “половинки” (призраки) крестиков и ноликов и появляются “обычные”, “классические” крестики или нолики.
Рассмотрим два разных возможных результата распутывания, которые может выбрать Боб.
Для примера, он начинает распутывать петлю с клетки №5 (центральная). Итак, в этой клетке Боб должен выбрать какой из сделанных ходов в эту клетку превратится из “призрака” в реальный ход и займет всю клетку. А выбор у Боба состоит из двух вариантов: X1 и X3, так как эти ходы входят в петлю, а вот призрак O2, который тоже находится в клетке 5 Боб выбрать не может, т.к. этот ход не содержится в петле.
Вариант 1.
Боб выбирает X3 в клетке №5.
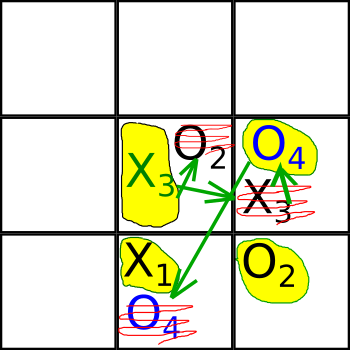
Тогда, в клетке №5 уже не должно быть X1, а значит ход X1 тем самым тоже определился с клеткой и в клетке №8 должен быть X1.
А раз так, то в клетке №8 не должно быть других призраков, не должно быть O4.
Значит раз клетка №8 для O4 запрещена, то этому нолику остается клетка №6.
А в клетке №6 был еще призрак хода X3, но мы же с него начали распутывание и с самого начала решили, что ход X3 будет в клетке №5.
От петли есть “отросток” в виде хода O2. Он тоже затрагивается в процессе распутывания. Так как в клетке №5 для O2 быть запрещено (мы уже сначала решили, что в этой клетке находится X3), то для O2 остается единственный вариант – клетка №9.
И вот результат распутывания – классические, обычные ходы, когда в каждой клетке полноценный крестик или нолик:
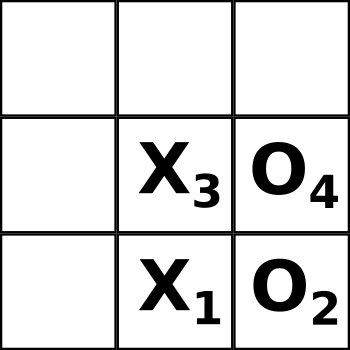
Вариант 2.
Боб выбирает X1 в клетке №5.
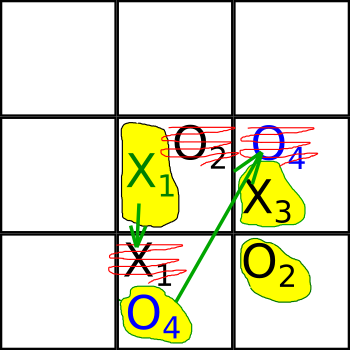
И в итоге результат распутывания выглядит так:
В примере выше петля состояла из трех разных клеток и для ее построения нужно было сделать три хода. Но самая простая петля может быть сделана одним игроком за один ход. Например, если бы Боб сделал свой первый ход так, что поместил две половинки X1 + X1 в одну пустую клетку, то это бы просто означало петлю в одной клетке с одним единственным вариантом распутывания:

Это обычный “классический” ход. Можно за два хода организовать петлю в двух клетках. Петля может быть и довольно большой, содержащей больше трех клеток. Однако, всегда есть только два варианта ее распутывания. Также стоит отметить, что одним ходом не получится замкнуть сразу две разных петли. Подсказка: сама процедура “распутывания” (квантовое измерение, коллапс) не должна оставлять после себя половинок “призраков”. Например, в приведенном выше примере, такая ситуация недопустима и означает, что распутывание не произведено до конца:
Тут в девятой клетке находится один призрак (половинка) от хода O2 (другую половинку в клетке №5 стерли во время распутывания). Так быть не должно, и вместо одинокой половинки мы должны нарисовать полноценный ход.
Итак, петлю закрыла Алиса, выбирает один из двух вариантов распутывания петли Боб, и если после распутывания игра не закончена, то Боб делает свой очередной ход.
Игра заканчивается так же, как и в обычных крестиках-ноликах, когда на поле имеется три полноценных (не половинки!) крестика или нолика в один ряд. Правда, есть одно отличие. Если игра заканчивается в результате распутывания нетривиальной петли (две и более клеток), то возможна ситуация, когда на поле одновременно появятся три крестика в ряд и три нолика в ряд. В этом случае правила предписывают посчитать индексы (номера ходов) у трех крестиков и трех ноликов. Тот, у кого сумма индексов меньше, тот и выиграл (получает 1 очко), а другой игрок, который как бы тоже выиграл, но у которого сумма индексов больше, получает 0.5 очка.
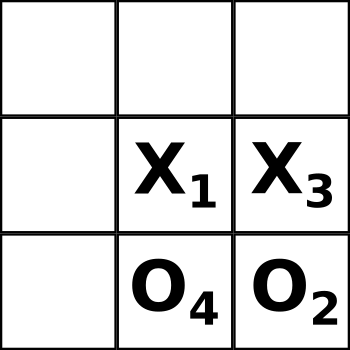
Проиллюстрируем это на примере. Итак, пусть после распутывания Бобом петли, которую закрыла Алиса, поле выглядит так:

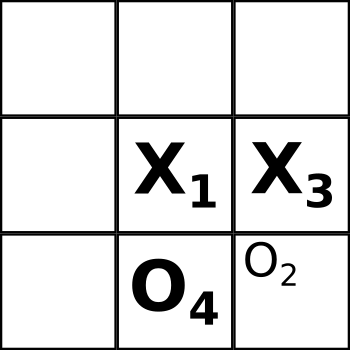
После распутывания, Боб делает свой ход крестиками в клетки 4 и 7 (хотя мог бы поставить оба крестика в клетку 4, сделав тем самым “классический” ход и выиграть):
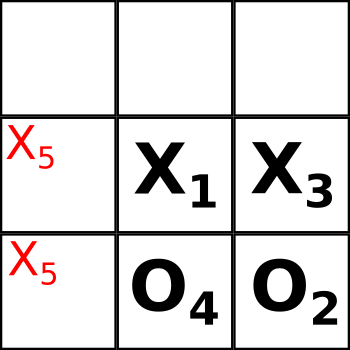
Алисе надоело играть и она делает свой ход ноликом в те же самые клетки 4 и 7, тем самым закрывая петлю из двух клеток:
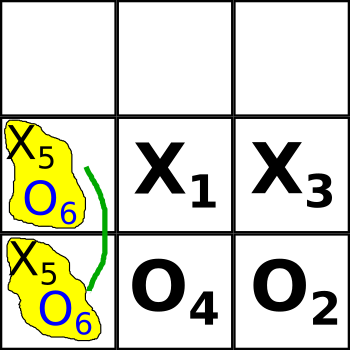
Боб тоже решил не растягивать игру и из двух вариантов распутывания выбрал тот, где крестик в клетке 4, а нолик в клетке 7 (в принципе, мог выбрать и вариант, когда нолик был бы в клетке 4, а крестик в клетке 7, что продолжило бы игру):
Мы видим, что в результате распутывания петли в клетках 4 и 7 получилось так, что и крестики и нолики какбы выиграли. Но теперь нужно сосчитать индексы:
- у крестиков: 5 + 1 + 3 = 9
- у ноликов: 6 + 4 + 2 = 12
Следовательно, по очкам крестики выигрывают. Боб, играющий крестиками, получает 1 очко, Алиса, играющая ноликами, получает 1/2 очка.
В рассмотренном выше варианте игры есть ограничения и проблемы:
- ходить можно только либо классически одним настоящим крестиком/ноликом в пустую клетку, либо разделив ход на две равноценные половинки. Пойти одновременно крестиком(ноликом) сразу в 9 клеток нельзя
- даже в случае хода двумя кретиками/ноликами нельзя распределить “вес” между ними, скажем этот крестик я сюда ставлю с “весом” 0.6, а этот – с “весом” 0.8.
- проблема “ничьей” и искусственного правила подсчета индексов
Другой, обобщенный, вариант игры в квантовые крестики нолики был предложен в работе: [J. N. Leaw and S. A. Cheong, Journal of Physics A: Mathematical and Theoretical, vol. 43, no. 45, 455304 (2010)]. В отличии от предыдущего варианта, в модифицированной версии максимальное число ходов равно числу клеток, т.е. девять. Однако, игра идет, можно сказать, в гильбертовом пространстве размерности 9. Базисом этого пространства служат классические ходы крестиков-ноликов.
Итак, каждый классический ход (каждую клетку) можно представить единичным базисным вектором ![]() в девятимерном пространстве. Вот так:
в девятимерном пространстве. Вот так:
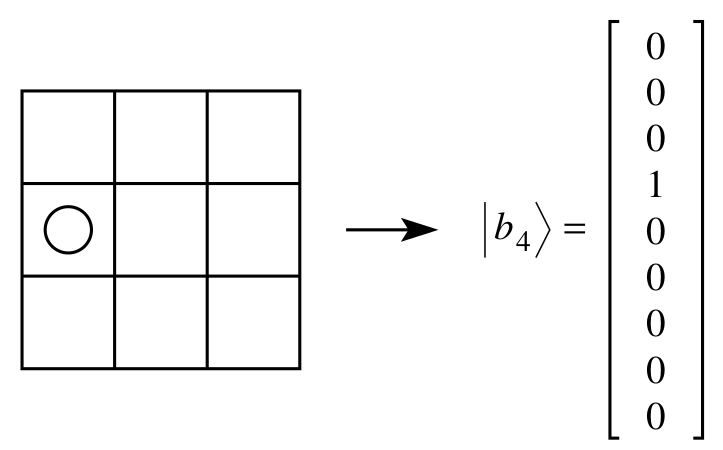
А каждый квантовый ход ![]() будет суперпозицией этих базисных векторов:
будет суперпозицией этих базисных векторов:
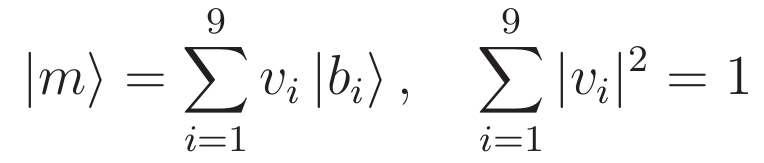
Важно, что как и каждый базисный вектор, так и каждый квантовый ход имеют единичную длину. Здесь величины ![]() – это проекции на координатные оси, а сумма их квадратов, соответственно, квадрат длины вектора. Теорема Пифагора точно так же работает и в девятимерном пространстве.
– это проекции на координатные оси, а сумма их квадратов, соответственно, квадрат длины вектора. Теорема Пифагора точно так же работает и в девятимерном пространстве.
Тем, кто помнит из школы как умножаются вектора, легко увидеть, что базисные векторы ![]() ортогональны (перпендикулярны) друг другу:
ортогональны (перпендикулярны) друг другу: ![]() , если
, если ![]() , и
, и ![]() .
.
Основная идея авторов состоит в том, что давайте потребуем, чтобы каждый квантовый ход ![]() был ортогонален всем предыдущим сделанным квантовым ходам.
был ортогонален всем предыдущим сделанным квантовым ходам.
Обратите внимание, это условие соблюдается в классических крестиках-ноликах, где каждый ход это не суперпозиция базисных векторов, а сами базисные вектора! То есть, привычные нам крестики-нолики – это частный случай квантовых крестиков-ноликов.
Указанное условие ортогональности ходов можно записать так:
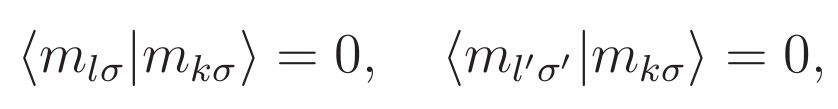
где ![]() – квантовый ход номер
– квантовый ход номер ![]() сделанный игроком номер
сделанный игроком номер ![]() (1 или 2). При этом:
(1 или 2). При этом: ![]() ,
, ![]() ;
; ![]() для первого игрока (делающего первый ход) и
для первого игрока (делающего первый ход) и ![]() для второго игрока.
для второго игрока.
Как понять, когда кто-то выиграл?
Пусть тройка чисел ![]() – это номера клеток, составляющие линию. Всего таких троек у нас может быть восемь: горизонтали {1,2,3}, {4,5,6}, {7,8,9}, вертикали {1,4,7}, {2,5,8}, {3,6,9}, диагонали {1,5,9},{3,5,7}.
– это номера клеток, составляющие линию. Всего таких троек у нас может быть восемь: горизонтали {1,2,3}, {4,5,6}, {7,8,9}, вертикали {1,4,7}, {2,5,8}, {3,6,9}, диагонали {1,5,9},{3,5,7}.
Для каждой такой тройки можно расчитать “вес” после хода ![]() игрока
игрока ![]() :
: ![]() . Для начала просуммируем все квантовые ходы, которые сделал игрок
. Для начала просуммируем все квантовые ходы, которые сделал игрок ![]() :
:
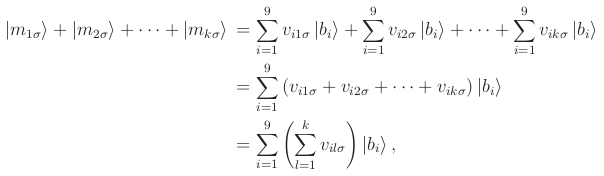
Затем определим:
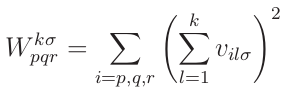
Тут ![]() – это вклад в амплитуду клетки номер
– это вклад в амплитуду клетки номер ![]() от хода номер
от хода номер ![]() который был сделан игроком
который был сделан игроком ![]() . В классических крестиках-ноликах
. В классических крестиках-ноликах ![]() равна или нулю или единице. В квантовом случае могут быть и другие числа.
равна или нулю или единице. В квантовом случае могут быть и другие числа.
Таким образом, игрок номер ![]() выигрывает после своего хода номер
выигрывает после своего хода номер ![]() , если хотя бы для одной из троек
, если хотя бы для одной из троек ![]() выполнено условие:
выполнено условие:
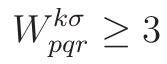
Очевидно, что игра в этот второй вариант квантовых крестиков-ноликов сопряжена с трудностями вычислительного характера. Так просто в уме ортогональность не проверишь, да и после каждого хода условие выигрыша тоже нужно проверять. Совершенно не понятна стратегия игры: какой первый ход лучше делать, и т.д.
Если в классических крестиках-ноликах всего есть около 20000 вариантов развития игры, то в нашем случае это число бесконечно велико, так как коэффициенты ![]() принимают непрерывный спектр значений.
принимают непрерывный спектр значений.