Не секрет, что в последнее время ведутся активные попытки построить квантовый компьютер. Вкратце, зачем это нужно. Доказано, что квантовый компьютер (когда будет построен) сможет за короткое время решать задачи, которые нынешние компьютеры (классические) могут решить лишь за тысячи лет непрерывной работы. Одной (и самой главной, из-за чего на исследования выделяются огромные деньги) из этих задач является нахождение простых множителей заданного числа (взлом шифрования с открытым ключом RSA). И, соответственно, создание новых, квантовых систем шифрования и защищенных линий связи. Возможен также и квантовый интернет, особенностью которого будут “запутанные” квантовые состояния, связывающие удаленные компьютеры между собой. А там, где новые компьютеры, там и новые игры.
В этом посте я попытаюсь рассказать о двух “квантовых” вариантах простой игры в крестики-нолики. Играть в эти квантовые крестики нолики можно без всякого квантового компьютера. Квантовые крестики-нолики в данном случае важны как методическое указание, как простейший пример того, что такое квантовая суперпозиция и редукция волновой функции при измерении. Итак, для начала определимся с игровым полем – это обычные 3х3 девять клеток. Для дальнейшего удобства пронумеруем их вот так:

Первый вариант игры, который мы рассмотрим, был предложен в работе [Allan Goff, Am. J. Phys. 74, 962 (2006)]. Суть заключается в том, что каждый игрок может имеющийся у него крестик (или нолик) не просто поставить в свободную клетку, а распределить его в двух разных клетках. Рассмотрим пример игры. Пусть крестиками играет Боб, а ноликами играет Алиса. Боб ходит первым и ставит свой первый крестик в клетки 5 и 8:
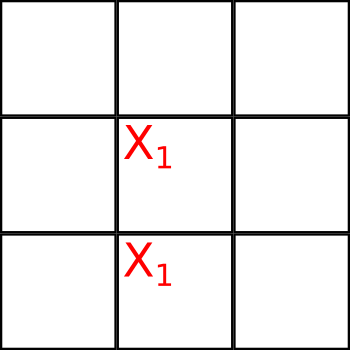
Здесь важно к крестикам/ноликам приписывать индексы – номера ходов.
Continue reading