На блог-платформе tumblr есть много интересных блогов, где помимо дизайнеров и прочих хипстеров выкладывают свои рисунки/анимации/идеи люди, увлеченные математикой. Все это в основном англоязычное, но понятное зачастую даже без всяких слов. Вот несколько картинок и идей, которые мне понравились.
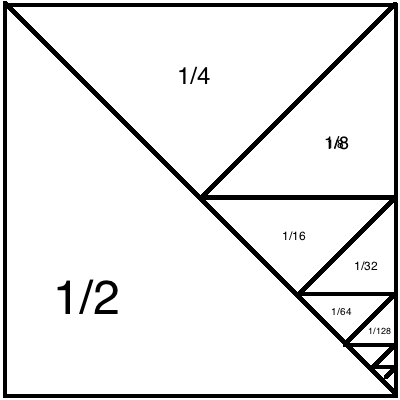
Наглядное доказательство:
Как получить синус и косинус из равномерно вращающейся по окружности точки:
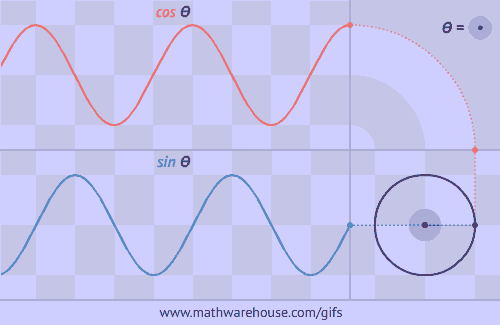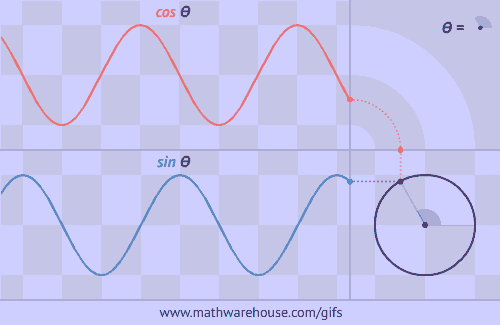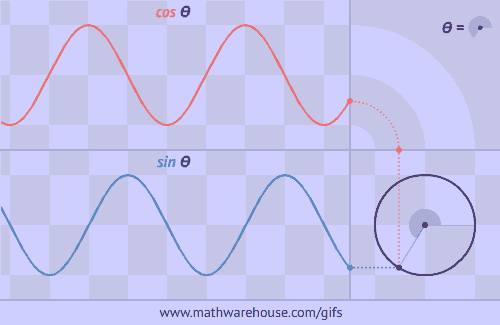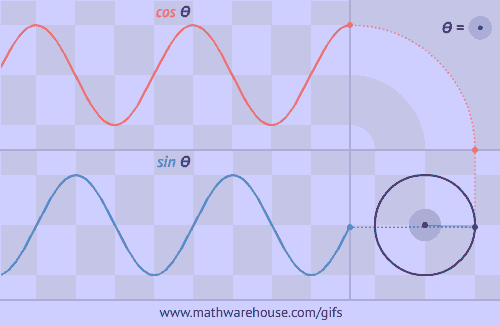
Как получить тангенс:
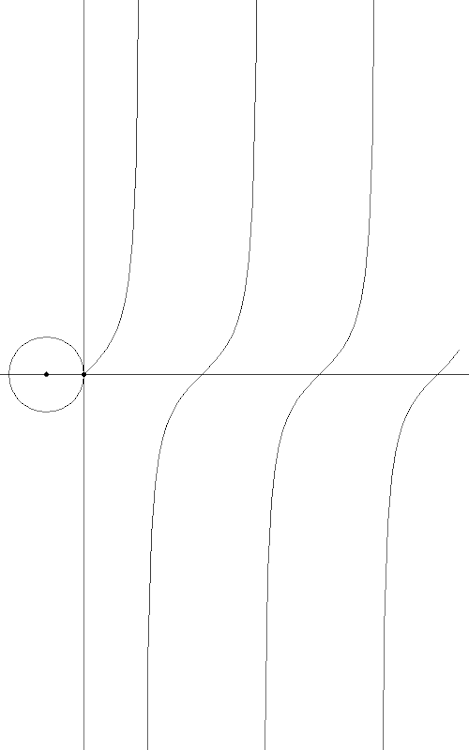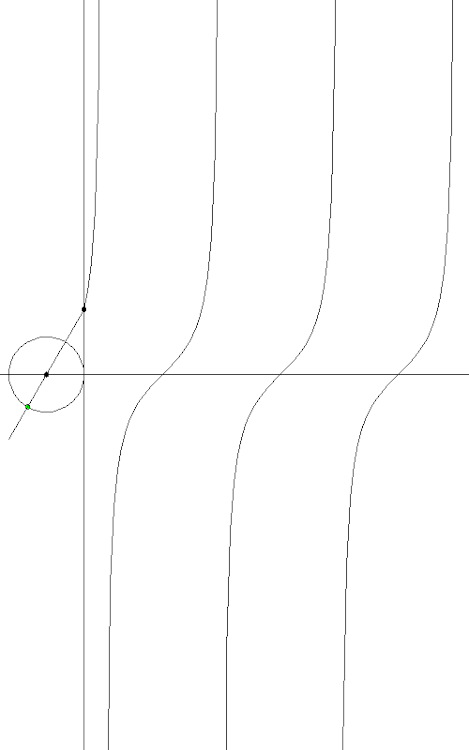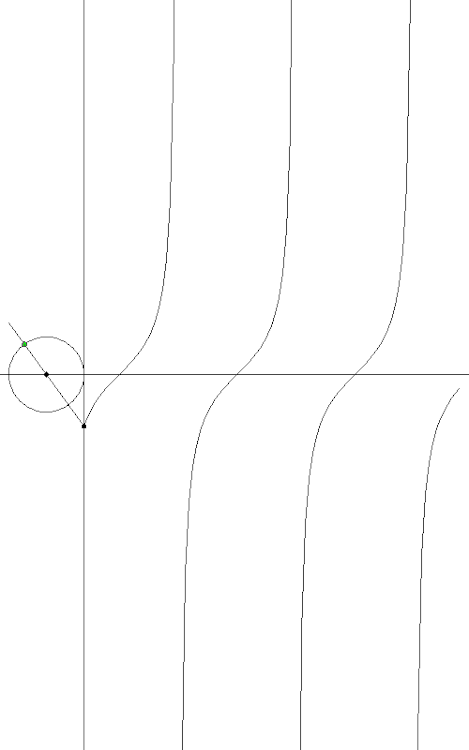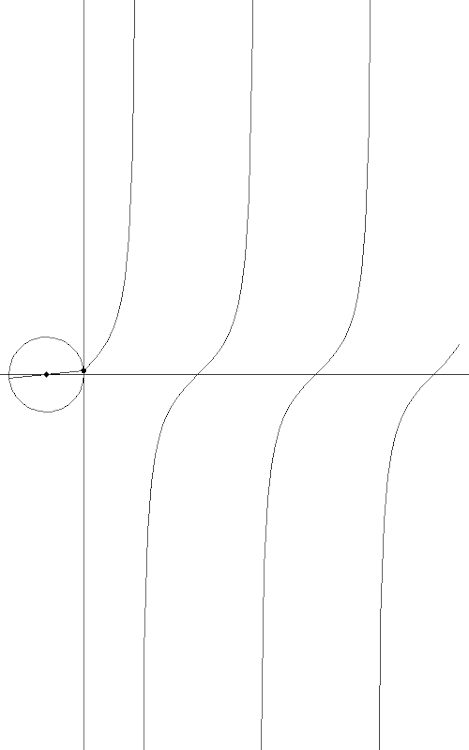
А вот если окружность не одна, а несколько и с разными скоростями вращения, то мы получаем наглядное представление о том, что такое преобразование Фурье, как сумма синусоид превращается в прямоугольные импульсы:
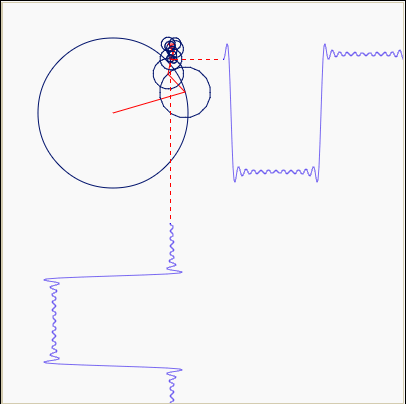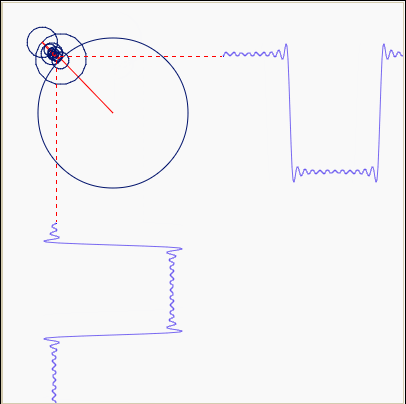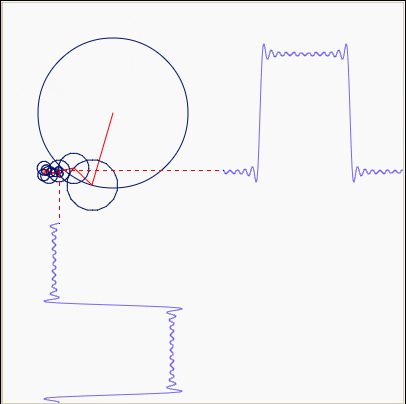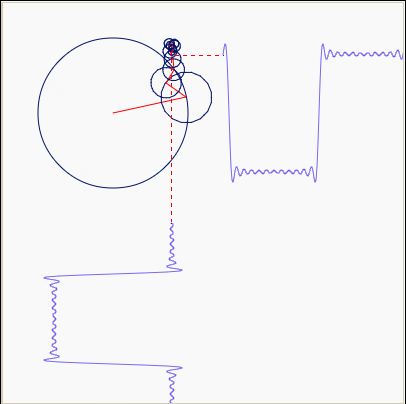
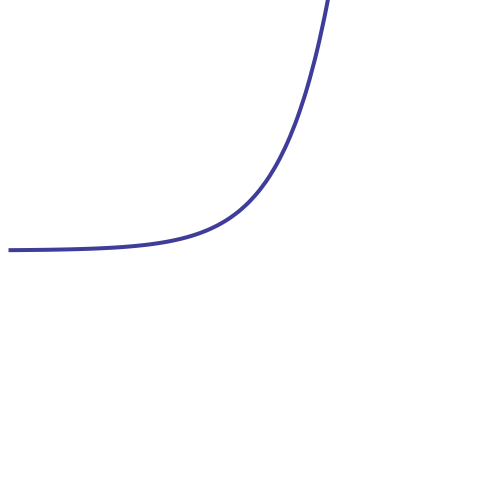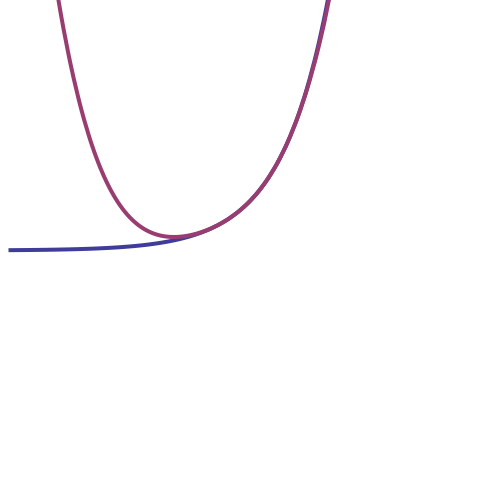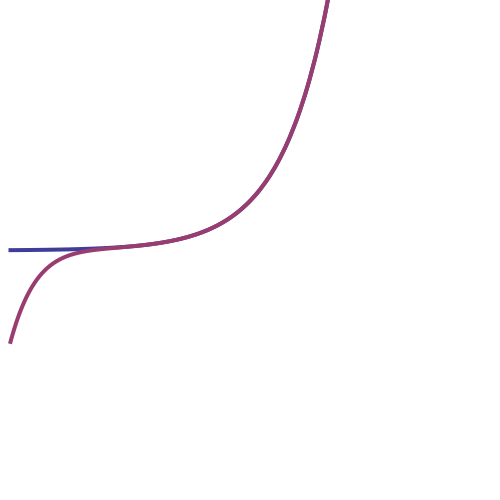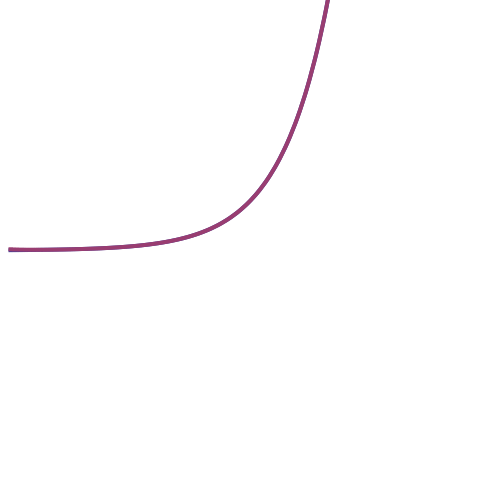
И теперь про разложение в ряд Тейлора. Вот наглядное изображение того, как график экспоненты аппроксимируется рядом:
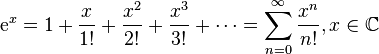
Наглядное доказательство того, что среднее геометрическое меньше либо равно среднему арифметическому:
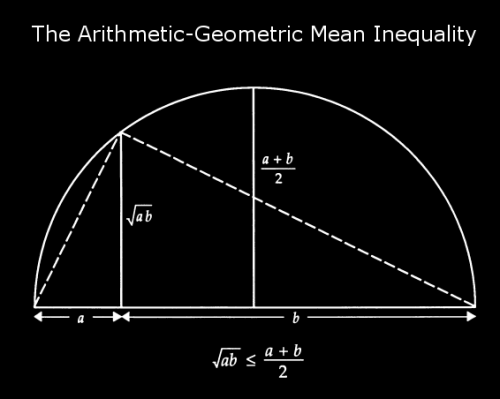
Золотое сечение определяется вот этим числом:
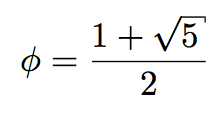
Оказывается, если возводить это число в целую положительную степень n, то результат будет все ближе и ближе к целому числу (дробная часть результата будет тем меньше, чем больший показатель степени):
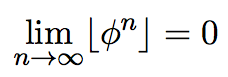
Это крайне простой и крайне неочевидный, поразительный факт. Я не удержался и в Питоне проверил для небольших значений n порядка 10 – 20. Сначала для золотого сечения, а затем для другого, близкого числа:
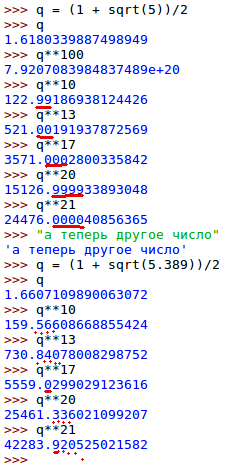
Удивительно!

И еще один занимательный факт. Пусть у нас есть генератор случайных чисел, равномерно распределенных в интервале от 0 до 1. Мы берем одно случайное число, затем второе и складываем. Если результат больше 1, то останавливаемся, если меньше 1, то берем третье случайное число и добавляем к сумме его, если результат опять меньше 1, то берем четвертое… Вопрос: сколько в среднем нужно взять таких случайных чисел, чтобы их сумма была больше единицы?
Ответ: e=2,718281828459045…
Поделиться: twitter facebook