Интересное рядом. Если Вам приходилось ездить на поездах по железной дороге, то глядя на рельсы Вы возможно задумывались о том, как именно они закругляются. То есть речь идет о том, что вот едет поезд по прямой, а потом начинает поворачивать – как именно? Вопрос оказывается не совсем тривиальным. Для начала напомню некоторые сведения из курса физики. Сила, действующая на тело (например, железнодорожный вагон) пропорциональна массе этого тела умноженной на ускорение, с которым это тело движется. Я специально записал формулировку таким образом: как бы наоборот, меняя причину и следствие, т.к. речь пойдет про неинерциальные системы отсчета. Понятно, что если мы говорим про толкание санок на льду, то нужно говорить, что благодаря приложенной силе санки начинают ускорятся. Но когда речь идет про пассажира, который падает с полки из-за резкого торможения поезда, то тут наоборот: эта невидимая сила, которая спихнула пассажира, вызвана ускорением поезда, в котором этот пассажир находился. Так вот, в самом начале развития железных дорог, когда скорости поездов были маленькими, вопрос про то как скруглять рельсы на поворотах не был так актуален. Можно было просто делать переход от прямого рельса к рельсу, который является частью окружности с нужным радиусом поворота R0.
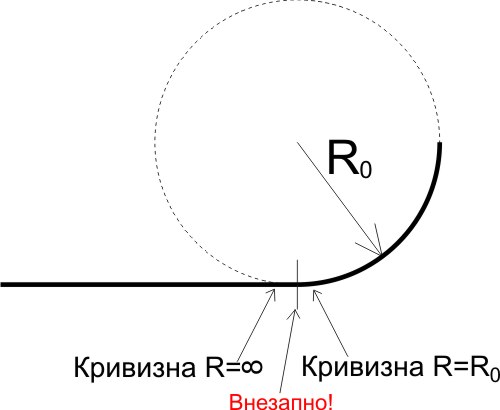
Однако, такой подход опасен тем, что при движении по такому железнодорожному полотну в момент перехода от прямого рельса к достаточно сильно закругленному на поезд начинает резко действовать центробежная сила. То есть по сути дела при движении по такой кривой происходит удар в сторону. Напомню, что центробежная сила равна:
(1)где
– скорость поезда, 
– радиус кривизны. Хочу отметить, что радиус кривизны, кривизна (кривизна = 1/радиус кривизны) – понятия, которые применимы не только к окружности, но и вообще к любой замысловатой кривой. В произвольной кривой, в отличии от окружности, радиус кривизны различен для разных точек данной кривой. Как найти радиус кривизны для произвольной точки кривой? Нужно взять две точки (красные точки на рисунке ниже) на кривой рядом с нужной нам (желтая), провести через эти точки касательные (красные) к кривой, затем через эти же точки провести перпендикуляры (синие) к касательным. Расстояние от точки пересечения перпендикуляров до кривой (зеленый отрезок) и будет радиусом кривизны.
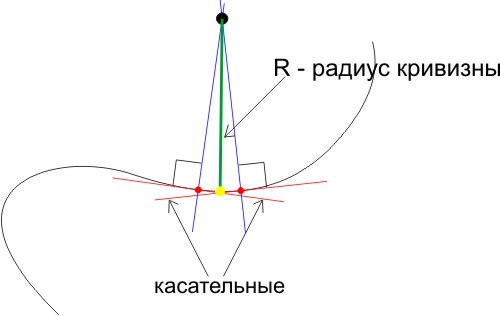
Естественно, читатели не знакомые с дифференциальным исчислением могут задаться вопросом: а конкретно до какой точки кривой (желтая на рисунке) нужно мерить расстояние от точки пересечения перпендикуляров? Ответ такой: если расстояние между красными точками (точками, в которых мы проводим касательные к кривой) стремить к нулю, то можно брать в качестве желтой точки на кривой любую из красных, они ведь все три будут бесконечно близко друг к другу. Итак, именно этот радиус кривизны
входит в формулу (1) для центробежной силы. И оттуда видно, что для прямой, у которой бесконечный радиус кривизны 
, центробежная сила равна нулю. То есть при движении поезда по прямому пути, резко переходящему в дугу окружности, получаем следующую зависимость центробежной силы от времени:
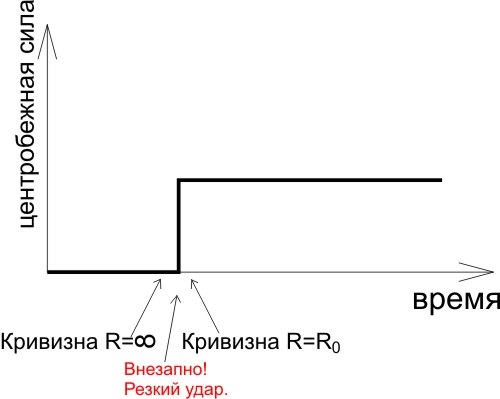
Видно, что сила появляется внезапно. А это плохо, внезапная сила по простому называется ударом, такой удар может сильно качнуть вагон и спровоцировать аварию. Поэтому при прокладке железнодорожных путей делают так, чтобы центробежная сила при движении по кривой нарастала постепенно:
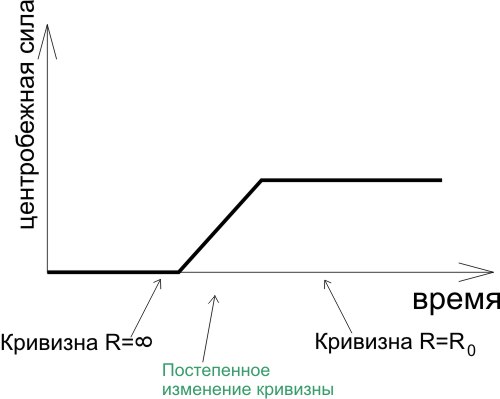
То есть между прямым участком с бесконечным радиусом кривизны и дугой окружности делают переходную кривую, радиус кривизны которой меняется от бесконечного до конечного. Например, это может быть кривая, которая задается выражением вида:
, что является аппроксимацией кривой, которая называется “клотоида”. Клотоида – это такая кривая, в которой кривизна (кривизна = 
) пропорциональна пройденному пути 
(при повороте руль поворачивается с постоянной скоростью). Повороты автомобильных скоростных трасс тоже делают по клотоиде, это, как утверждает википедия, позволяет проходить такие повороты практически без снижения скорости.
Вот таким способом мат.анализ и дифференциальная геометрия становятся полезными в народном хозяйстве 🙂
Поделиться: twitter facebook