Написать эту заметку меня побудила работа сео блогера Webpavilion в которой он анализирует собранную им статистику апдейтов Яндекса. Он предоставил у себя текстовые файлы с датами апдейтов выдачи и ТИЦ, чем я и воспользовался. Я решил провести статистическое исследование этих данных и сравнить их с известным из статистики пуассоновским распределением случайной величины.
Первое что я сделал, это данные в формате 23.03.2009 перевел в формат одного числа. Делалось это по формуле 365*год + 30*месяц + день, все это я записываю в массив A[i]. Далее я создаю другой массив D[i], такой, что
D[i] = A[i+1] – A[i].
Таким образом, я получил массив, в котором записаны промежутки в днях между апдейтами. Тут, конечно, есть неточности, из-за того, что я не стал учитывать то, что в некоторых месяцах 31 день, 2008 год – был високосным, благо, данных много и ошибка будет маленькая.
Далее я работаю только с массивом D[i], т.к. именно в нем вся полезная информация (будем считать, что Яндекс работает одинаково зимой и летом). Первое, что можно сделать – это найти среднее значение D[i]. Оно получилось равным 3.7 дней. Затем, имея среднее, можно вычислить дисперсию – среднее отклонение от среднего. Дисперсия получилась равной 2.57 дней.
Теперь можно построить функцию вероятности P(t), где t – измеряется в днях.
| Число дней | Вероятность того, что между апдейтами будет это число дней |
| 1 | 11.627906976744% |
| 2 | 25.369978858351% |
| 3 | 21.353065539112% |
| 4 | 15.221987315011% |
| 5 | 10.359408033827% |
| 6 | 5.9196617336152% |
| 7 | 3.1712473572939% |
| 8 | 1.9027484143763% |
| 9 | 1.0570824524313% |
| 10 | 1.0570824524313% |
| 11 | 0.84566596194503% |
| 12 | 0.84566596194503% |
| 13 | 0.21141649048626% |
| 14 | 0.21141649048626% |
| 15 | 0.21141649048626% |
| 16 | 0.21141649048626% |
| 17 | 0% |
| 18 | 0% |
| 19 | 0.42283298097252% |
| 20 | 0% |
Сравним эту функцию с распределением Пуассона, в котором в качестве параметра поставим найденное из данных по яндексу среднее (3,7 дней), дисперсию (2,5 дней), и среднее между средним и дисперсией (3,1 дней).
Дело в том, что в распределении Пуассона среднее должно быть равно дисперсии, а у нас из опытных данных они не равны. Но мы тем не менее посмотрим на графики:
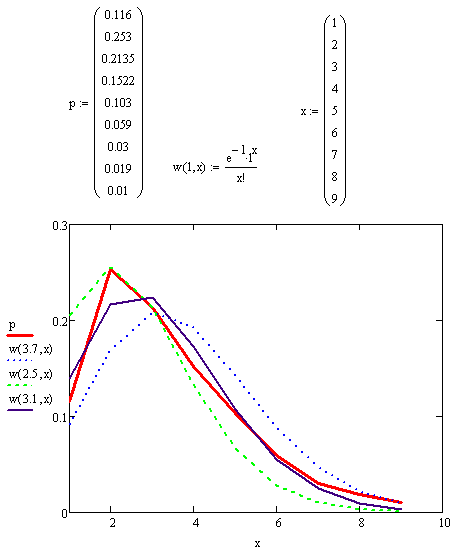
На графике: x – количество дней, P (красная сплошная линия) – данные реальных апдейтов, w(l,x) – функция распределения Пуассона (l – параметр распределения).
Как видно из графика, есть качественное совпадение хода кривых. Наибольшее совпадение наблюдения и распределения Пуассона наблюдается при параметре 3,1 день. Хочется сказать такое оправдание: погрешность исходных данных составляет порядка 0,5 дня, т.к. начало АПа в час ночи или в 11 вечера соответствует одному и тому же дню, хотя реальная разница около суток.
Теперь построим функцию распределения f(t), где t – количество дней. Ее смысл такой: f(t) это вероятность того, что случится АП, если ждать t дней. Естественно, что при очень больших t, f(t) должна стремиться к 1. Ниже представлен график, на котором изображена функция распределения, полученная из наблюденных данных (красная кривая), и функция распределения, полученная из распределения Пуассона с параметром, равным среднему из наблюденных данных (3,7 дней).
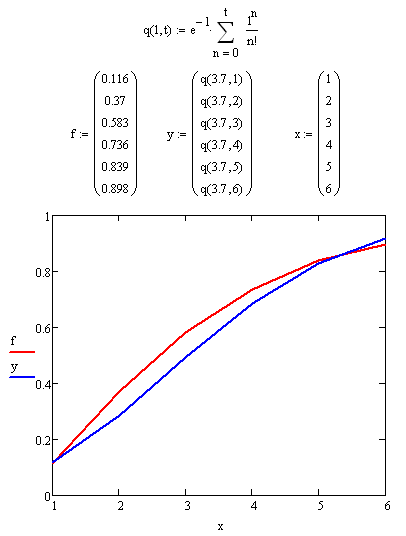
Какой вывод можно сделать? Очевидно, что Яндекс – развивающаяся система, и его параметры конечно же зависят от времени, чего в данном рассмотрении не учитывалось. Конечно, Яндекс не может быть идеально случайным. Но все таки качественно ход кривых на графиках похож, при чем еще раз подчеркну: функция, которая описывает поведение Яндекса
1) взята не “с потолка”, это всем известное распределение. Ему подчиняются очень многие явления нашей жизни.
2) параметр в эту функцию подставлен тоже не совсем “с потолка” лишь бы подогнать под наблюдаемые данные, параметр соответствует среднему значению, рассчитанному из наблюдаемых данных.
Таким образом, можно утверждать, что Яндекс – сложная динамическая система, которая связана с еще более сложной системой – интернетом. А в сложных системах с большим числом переменных могут наблюдаться статистические закономерности, которые универсальны для любых стохастических систем.
PS/ После некоторых размышлений я пришел к выводу, что написанное мной выше, касаемое распределения Пуассона – неправильно. Продолжение в следующей серии.
Вот график функции распределения Апдейтов:

Можно сказать, что регулярные апдейты Яндекса – не случайны, а вот задержки имеют уже характер случайностей. Поделиться: twitter facebook