Я не являюсь любителем SEO, этой туевой хучи SEO блогов всяких крыжопольских сео-бомжей про заработок в интернете, продвижение сайтов, личностный рост, и блоги про то, как надо вести блоги. Но мне интересны математические аспекты ранжирования сайтов, как именно думали инженеры поисковой системы (Яндекса), создавая алгоритмы ранжирования и ТИЦ. В большинстве т.н. SEO блогов рекомендации похожи на какие то шаманские рецепты – все рассматривается качественно, но не количественно. А мне стало интересно попробовать рассмотреть какой нибудь мелкий SEO вопрос с количественной стороны. Конечно, ответ будет не правильный, т.к. во-первых, я не знаю всей информации, не знаю реального алгоритма, и во-вторых, даже если бы и знал – реальный алгоритм наверняка очень сложный, поэтому в данной работе используется простая неправильная эмпирическая модель подсчета ТИЦ. Пользуясь этой моделью были указаны условия, при которых взаимный обмен ссылками для обоих сайтов является эффективным.
Для нормального просмотра формул и обозначений должен быть не отключен JavaScript.
ТИЦ (Тематический Индекс Цитирования) – некое число, которое сопоставляется сайту. Это число тем больше, чем больше ссылок на данный сайт с других сайтов, и тем больше, чем больше ТИЦ этих других, ссылающихся сайтов.
Предположим, что ТИЦ i-того сайта рассчитывается по следующей формуле:
$ t_i=Cfrac{displaystylesum_{kne i} l_{ki}(t_k + t_0)}{displaystyle {D + sum_{kne i}l_{ik}(t_k + t_0)^{-1}} } $ (1)
Где ( t_i ) – значение ТИЦ ( i )-того сайта, ( l_{ki} ) – количество ссылок с сайта ( k ) на сайт ( i ), ( t_0 ) – некое значение ТИЦ, постоянное для всех сайтов, можно считать его равным ТИЦ=10, ( C,D > 0) – некие константы. Суммирование ведется по всем сайтам, исключая данный.
Как видно из выражения (1) ТИЦ сайта тем больше, чем больше на сайт ссылок с сайтов с высоким ТИЦ. Знаменатель в (1) написан таким образом, что бы уменьшать ТИЦ сайта, если данный сайт ссылается на другие сайты. Причем, чем выше ТИЦ сайтов, на которые стоят ссылки, тем меньше забирается ТИЦ. Другими словами, ссылка на vkontakte практически не отнимет ТИЦ, а вот ссылка на сайт с ТИЦ=0 уменьшит собственный ТИЦ значительнее. Для ситуации, когда сайт вообще ни на кого не ссылается, в знаменателе стоит константа ( D ), что бы не возникало ситуации с равным нулю знаменателем. Мы предполагаем, что ТИЦ не может быть меньше нуля.
Пусть имеются два сайта с номерами ( n_1, n_2 ), которые производят обмен ссылками. Обмен прямой, по одной ссылке друг на друга. Обозначим значения ТИЦ этих сайтов соответственно ( t_{n_1}, t_{n_2} ). Используя формулу (1) найдем приращение ТИЦ ( delta t_{n_1} ), вызванное обменом, для сайта ( n_1 ).
$ delta t_{n_1} = t_{n_1} (mathrm{after;exchange}) – t_{n_1} (mathrm{before;exchange})$
$ delta t_{n_1} = Cfrac{displaystylesum_{kne n_1} l_{kn_1}(t_k + t_0)}{displaystyle {D + sum_{kne n_1}l_{n_1k}(t_k + t_0)^{-1}} } – Cfrac{displaystylesum_{kne n_1,n_2} l_{kn_1}(t_k + t_0)}{displaystyle {D + sum_{kne n_1,n_2}l_{n_1k}(t_k + t_0)^{-1}} } $ (2)
Выражение (2) можно преобразовать, выделив в первом слагаемом из сумм слагаемые, которые содержат сайт ( n_2 ). В результате получаем:
$ delta t_{n_1} = Cfrac{displaystyle t_{n_1}}{displaystyle{ 1 + gamma_{n_1, n_2} } }left(frac{displaystyle{t_{n_2}+t_0}}{displaystylesum_{kne n_1, n_2} l_{kn_1}(t_k + t_0) } – gamma_{n_1, n_2} right) $ (3)
где обозначено
$ gamma_{n_1, n_2} = frac{displaystyle 1}{displaystyle(t_{n_2} + t_0)left(D + sum_{kne n_1,n_2}l_{n_1k}(t_k + t_0)^{-1}right) } $
Потребуем, что бы прирост ТИЦ для сайта ( n_1 ) был положительным:
$ delta t_{n_1} > 0 $
Как нетрудно увидеть, в этом случае из (3) следует условие:
$ t_{n_2} + t_0 > frac{displaystylesum_{kne n_1, n_2} l_{kn_1}(t_k + t_0) } {displaystyle(t_{n_2} + t_0)left(D + sum_{kne n_1,n_2}l_{n_1k}(t_k + t_0)^{-1}right)} $
Или, используя (1), получаем:
$ t_{n_2} > asqrt{t_{n_1}} ,-, t_0 $ (4)
Из соображений симметрии задачи, легко сразу написать такое же условие положительности прироста ТИЦ после обмена для сайта ( n_2 ):
$ t_{n_1} > asqrt{t_{n_2}} ,-, t_0 $ (5)
где ( a = 1/sqrt{C} ).
Проанализируем условия (4), (5) и подумаем, какое значение нужно приписать константе ( a ). Рассмотрим частный случай, когда ТИЦ обоих сайтов, участвующих в обмене, одинаковый. В этой ситуации, наша простая модель предусматривает в общем случае 2 варианта событий: после обмена ТИЦ обоих сайтов возрастет, или же упадет. Из (4) и (5), а также из предположения, что ( t_0=10 ) легко получить, что предельный по вредности коэффициент ( a ) будет равен ( sqrt{40} ), в этом случае при обмене ссылками между сайтами с одинаковым ТИЦ никогда не будет падения ТИЦ после обмена, однако в большом диапазоне ТИЦ (малые ТИЦ) такой обмен будет невыгоден для одного из участников, если имеется небольшое различие ТИЦ. Эта ситуация проиллюстрирована на графике ниже:
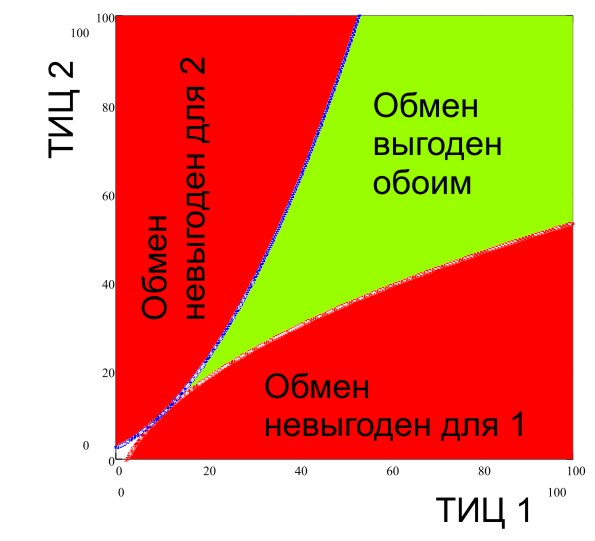
Если Яндекс “прикрутил гайки” ( ( a=10 ) ), то значение константы соответствует тому, что для некоторых небольших ТИЦ взаимообмен чреват понижением ТИЦ у обоих сайтов (черная область на графике ниже):
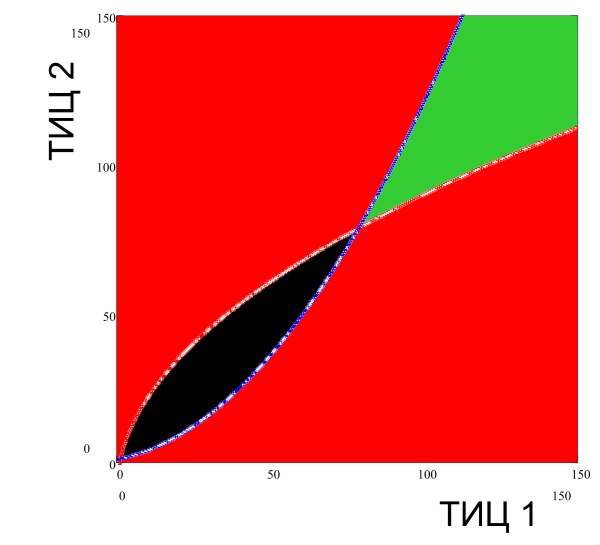
Если реальность более благосклонна к обмену и диаграмма целесообразности выглядит примерно так ( ( a=4 ) ):
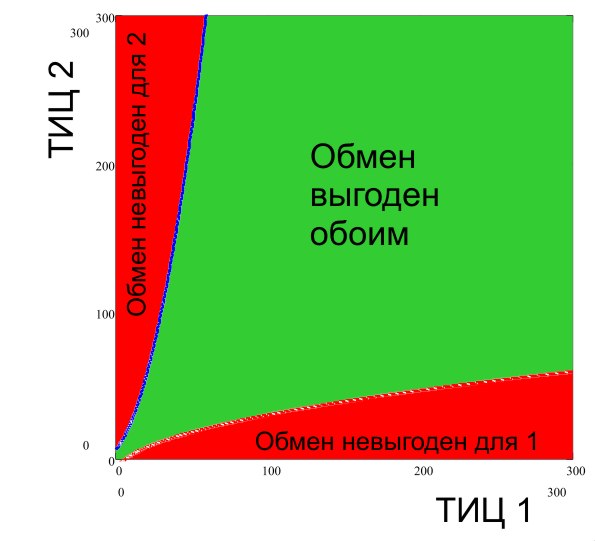
Некий итог: к сожалению, результат оказался зависящим от константы, которая должна подбираться эмпирическим путем, однако для этой константы имеется характерное значение, которое соответствует предельному случаю “закрученных гаек”, но при котором меняющиеся сайты с одним и тем же ТИЦ никогда не уменьшат свой ТИЦ из-за обмена. Поэтому для быстрой оценки эффективности прямого обмена ссылками необходимо посмотреть, выполняется ли неравенство:
$ t_{mathrm{partner}} > 6sqrt{t_{mathrm{your}}} ,-, 10 $
где ( t_{mathrm{partner}} ) – ТИЦ сайта с которым меняется Ваш сайт, ( t_{mathrm{your}} ) – ТИЦ Вашего сайта. Если неравенство выполняется, то обмен выгоден для Вашего сайта. Поделиться: twitter facebook