В связи с событиями на АЭС Фукусима начался очередной виток пропаганды отказа от АЭС. В Германии даже собираются останавливать свои АЭС старой постройки (до 1980 года). Зеленые говорят о том, что нужно переходить на безопасные источники энергии – ветер, солнце, вода. Однако, что бы не утверждали экологи, в масштабах страны такой переход не возможен. Но я уже давно вижу на территории частных домов установленные ветрогенераторы. Недавно меня заинтересовал вопрос о том, сколько энергии максимально можно получить из ветряка?
Очевидно, что вопрос нужно ставить так: какую максимальную мощность может развить ветрогенератор с определенным размером лопастей при определенной скорости ветра и плотности воздуха? Ниже я попытаюсь рассмотреть данную задачу, и теоретические изыскания сравню с реальными данными, которые я нашел на харьковском сайте, предлагающем альтернативные источники энергии для населения.
Итак, пусть площадь, которую покрывают лопасти ветряка при вращении равна 
(
, где 
– то, что называют “диаметр ротора”). Скорость ветра 
будем считать постоянной, не зависящей от координат и времени. Рассмотрим воображаемый цилиндр, одно из оснований которого, площадью – это ротор ветряка, а другое – удалено от ротора на расстояние 
против ветра. Бока цилиндра параллельны направлению скорости ветра.
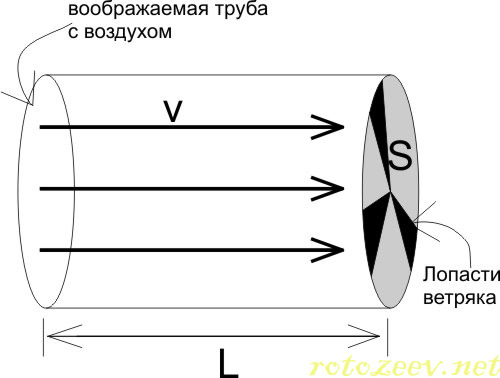
Посчитаем кинетическую энергию воздуха, заключенного в данном цилиндре. Кинетическая энергия рассчитывается по известной школьной формуле:
.Что такое
– понятно, это скорость ветра. А что такое 
? Это масса воздуха, заключенного в данный цилиндр, и она равна объему цилиндра 
умноженному на плотность воздуха 
. Итак:
. (1)Но нам нужна мощность ветряка, а не энергия воздуха в воображаемом цилиндре. Пусть этот воображаемый цилиндр пройдет сквозь плоскость ветряка за время
, тогда мы можем написать, что мощность, которую мог бы отобрать ветряк из кинетической энергии воздуха в цилиндре, равна
. (2)А теперь давайте присмотримся к букве
, ее можно выразить через уже ранее введенные буквы. Ведь – это время, за которое цилиндр, движущийся со скоростью пройдет расстояние равное своей длине . То есть 
. Подставим это в (2), используя при этом (1):
. (3)Таким образом, мы видим, что максимально возможная мощность ветряка пропорциональна кубу скорости ветра.
Теперь сравним теоретически рассчитанную максимальную мощность, даваемую формулой (3) с мощностью, которую дает реальный ветряк.
Пусть плотность воздуха равна 
кг/м3
Скорость воздуха равна 
м/с
Диаметр ротора 
м, т.е. 
м2
На сайте написано, что при таких условиях мощность, выдаваемая ветрогенератором будет составлять 1,6 кВт. Максимально возможная мощность по формуле (3), получается примерно 4,7 кВт. Итого, КПД получается равным 
, что составляет примерно 34%. Довольно неплохо. Я думал, что будет меньше.
Так же интересно посмотреть на зависимость выдаваемой мощности от скорости ветра, которую я позаимствовал с указанного выше сайта:
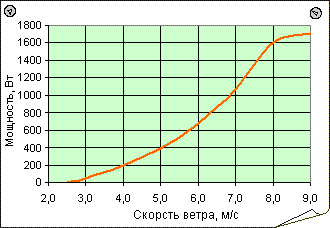
Видно, что при скоростях ветра менее 8 м/с мощность растет действительно как куб скорости! Например, значение мощности при
м/с(когда скорость в два раза меньше 8 м/с) составляет 
Вт, что в два в кубе раз меньше. Это значит, что при малых скоростях ветра КПД ветряка не зависит от скорости ветра. А при сильном ветре по видимому уже вступают в игру нелинейные эффекты, турбулентности, рост трения и т.п. факторы.
Надеюсь, изложенные тут размышления и теоретизирования кому нибудь помогут.
Поделиться: twitter facebook