Как выигрывать в рулетку

Если Вы серфите по разным сайтам, то Вы наверняка видели завлекающие тизеры, на которых зачастую изображен довольный паренек и надпись “Он рубит бабло в интернете и готов поделиться секретом!”, “100$ в день – легко!”, “А я заработал в инете на машину”, “Ушел с работы, гребу лопатой бабло в интернете!” и т.п. Кликая на такие объявления Вы в основном попадаете на сайты людей, якобы раскрывающих секреты беспроигрышной игры в рулетку (ну и далее реферальная ссылка на онлайн казино). Их “секрет” для непосвященного человека выглядит довольно убедительным, я и сам в детстве дошел до такого очевидного алгоритма. Суть в следующем. Будем ставить на красное/черное (чет/нечет, 1-18/19-36), то есть делать такие ставки, при выигрыше которых сумма удваивается. Естественно, что и вероятность выигрыша таких ставок равна 1/2 (18/37, если быть точным, т.к. имеется “0”, но эта деталь не существенна). И вот мы ставим 1S денег (это буква S, а не доллар. S может быть равно чему угодно – хоть 10 гривен, хоть 97 евро). Если выиграли, то получили 2S – хорошо, если проиграли, то ставим уже 2S денег. Опять, если выиграли в этот раз 4S, то мы получается отыгрываемся за 1й неудачный раз 1S, возвращаем то, что поставили сейчас 2S и получаем законный чистый выигрыш с двух партий 1S (1S+2S+1S=4S). Ну и так далее: если и во второй раз проиграли, то ставить надо уже 4S денег, и при удачном исходе мы опять отыгрываемся + получаем 1S чистого выигрыша, если же каким то чудом снова проиграли, то в следующий раз надо ставить 8S денег… После выигрыша надо обязательно возвращаться к ставке в 1S. Ну и, казалось бы, что имея в запасе некоторый резерв денег и играя по такой системе можно ходить в казино как на работу. Покажем теперь, почему эта схема заработка на жизнь не будет работать.

Итак, для простоты примем то, что в день Вам нужно заработать $S$ денег. И начинать игру Вы также будете с суммы в $S$ денег. Пусть также у Вас есть запас денег, достаточный для того, чтобы $N-1$ раз подряд потерпеть неудачу и на $N$ -ный раз все таки выиграть и заработать свое $S$ количество денег. Для этого Вам нужно иметь:

$\Large{S + 2S + 4S + \dots + 2^{N-1}S = 2^NS}$

Пусть Вы хотите таким образом зарабатывать в течении 20 лет. Это получается порядка 8000 дней. Столько раз должна сработать Ваша схема. Обозначим для дальнейшего это число буквой $M$ .

Вероятность выигрыша в рулетку при ставке на красное/черное равна $P_{1win}=18/37$ , ну и, соответственно, вероятность проиграть в этом случае

$\Large{ P_{1loose}=1 - P_{1win} }$

Пусть начался очередной день игры. Вероятность того, что мы сегодня $N$ раз подряд проиграем (потратив весь запас) равна:

$\Large{ P_{day-loose} = P_{1loose}^N }$

Ну и, соответственно, вероятность того, что это прискорбное событие сегодня не произойдет (то есть мы, как и предписано стратегией, получим свои $1S$ денег и уберемся из казино) равна

$\Large{ P_{day-win} = 1 - P_{day-loose} }$

Но нам нужно, чтобы мы выигрывали каждый день, в течении $M$ дней. Вероятность того, что мы в течении этих $M$ дней ни разу не проиграемся будет равна:

$\Large{ P_{total-win} = P_{day-win}^M }$ (1)

Уже отсюда видно, что вероятность проиграться есть всегда. Из приведенных формул не следуют вероятности 0 или 1. Но попытаемся кое что извлечь из полученных формул. Найдем, или точнее – оценим число $N$ . Положим для простоты, что вероятность не проиграться за $M$ дней близка к 1 (мы ведь этого добиваемся). То есть:

$\Large{ P_{total-win} = 1 - \varepsilon, \;\;\; \varepsilon<<1 }$

Тогда, используя (1), получим:

$\Large{ 1 - \varepsilon = P_{day-win}^M }$ (2)

Возьмем логарифм от обеих частей равенства (2):

$\Large{ - \varepsilon = M\,ln{P_{day-win}} }$

или

$\Large{ ln{(1-P_{day-loose})} = - \frac{\displaystyle\varepsilon}{\displaystyle M} }$ (3)

(Тут использовано то, что $\ln(1+x)\approx x$ при $x<<1$ и вместо значка $\approx$ я просто написал $=$ )
Возведем экспоненты в степени, равные левой и правой частям (3) и приравняем их:

$\Large{ 1-P_{day-loose} = \exp(-\frac{\displaystyle\varepsilon}{\displaystyle M}) }$ (4)

В выражении (4) экспоненту справа можно разложить по малому параметру $\varepsilon$ :

$\Large{ \exp(-\frac{\displaystyle\varepsilon}{\displaystyle M})\approx 1-\frac{\displaystyle\varepsilon}{\displaystyle M} }$ (5)

Используя (5) можем переписать (4) в виде:

$\Large{ P_{day-loose} = \frac{\displaystyle\varepsilon}{\displaystyle M} }$

Или, вспоминая определение $\large{P_{day-loose}}$ :

$\Large{ P_{1loose}^N = \frac{\displaystyle\varepsilon}{\displaystyle M} }$ (6)

Взяв логарифмы от обеих частей равенства (6) получаем для $N$ выражение:

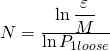$\Large{ N = \frac{ \displaystyle{\ln{\frac{\displaystyle\varepsilon}{\displaystyle M}} }}{\displaystyle{ \ln{P_{1loose}} }} }$ (7)

Возьмем для примера

$\Large{ \varepsilon=0.01 }$

Тогда, из формулы (7) следует, что для того, чтобы за 8000 дней игры была 99% вероятность успеха стратегии нужно, чтобы $N$ было равно 18. Много это или мало? Это очень много. Это значит, что для того, чтобы зарабатывать в казино каждый день $S$ денег, вам нужно иметь каждый день с собой в кармане $2^{18}S$ денег. Это уже огромная сумма. Хотите зарабатывать в казино каждый день 100 доларов на протяжении 20 лет? Будьте добры: имейте при себе каждый день 260000000 долларов.

Пусть даже у Вас есть нужные $2^{18}S$ денег. Давайте прикинем: за год игры в казино Вы заработайте $365\,S$ денег. А если Вы положите эти же $2^{18}S$ денег в банк, пусть, для простоты расчетов, под 3,125% годовых (3,125% соответствует $1/32=1/2^5=2^{-5}$ ). Тогда заработок в банке составит $2^{18}2^{-5}S=2^{13}S=8192S$ , что в 22 раза выгоднее, чем играть в казино с тем же запасом денег в кармане.

То есть мы видим, что в описанной выше стратегии игры от глаз наивных манимейкеров спрятан закон больших чисел. Если есть банка варенья, то можно попробовать ложку – варенья останется в банке практически столько же, сколько и было. Но если брать по ложке в день, то банка все таки станет пустой.

Поделиться: twitter facebook

Свежие записи блога

Счетчики:

Свежие записи блога

О чем я тут пишу:

Счетчики: